At present, Dr. Juan (Jane) Cao is a professor at School of Mathematical Sciences, Xiamen University. She received her B.S. degree in Information and Computing Science from Department of Mathematics, Fuzhou University, in June 2004. She received her Ph.D. degree in Applied Mathematics from Zhejiang University under supervision of Prof. Guozhao Wang, in June 2009. During Oct. 2007 and Oct. 2008, she was a visiting scholar at Department of Computer Science, The State University of New York at Stony Brook (Stony Brook University), under supervision of Prof. Hong Qin. During Sept. 2017 and Sept. 2018, she was a visiting scholar at Department of Mechanical Engineering, Carnegie Mellon University.

(招收研究生) I am looking for intelligent, self-motivated, and dedicated graduate students. If you are interested in my research directions, please feel free to contact me.

Computer aided geometric design, Digital geometry processing for computer graphics

 

---

	Polygonal Finite Element-Based Content-Aware Image Warping  Juan Cao*; Xiaoyi Zhang; Jiannan Huang; Yongjie Jessica Zhang Computational Visual Media, 2023, 9(2): 367-383
	Classification of Polynomial Minimal Surfaces  Lincong Fang, Yingli Peng, Yujun Li, Juan Cao* Computer Aided Geometric Design (Proc. GMP), 2022, 96: 102106
	Image Representation on Curved Optimal Triangulation  Yanyang Xiao, Juan Cao, Zhonggui Chen Computer Graphics Forum, 2022, 41(6): 23-36
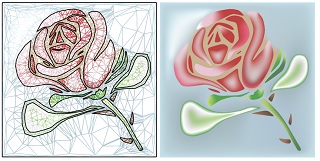	TCB-Spline-Based Image Vectorization  Haikuan Zhu, Juan Cao*, Yanyang Xiao, Zhonggui Chen, Zichun Zhong, Yongjie Jessica Zhang ACM Transactions on Graphics, 2022, 41(3), Article No. 34: 1-18
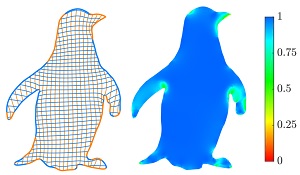	TCB-Spline-Based Isogeometric Analysis Method with High-Quality Parameterizations  Zhihao Wang, Juan Cao*, Xiaodong Wei, Yongjie Jessica Zhang Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114771
	Quadratic Serendipity Element Shape Functions on General Planar Polygons  Juan Cao*, Yi Xiao, Yanyang Xiao, Zhonggui Chen, Fei Xue, Xiaodong Wei, Yongjie Jessica Zhang Computer Methods in Applied Mechanics and Engineering, 2022, 392: 114703
	Merge-Swap Optimization Framework for Supervoxel Generation from Three-Dimensional Point Clouds  Yanyang Xiao, Zhonggui Chen, Zhengtao Lin, Juan Cao, Yongjie Jessica Zhang, Yangbin Lin, Cheng Wang Remote Sensing, 2020, 12(3), 473  [DOI]
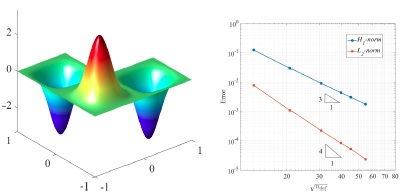	A Finite Element Framework Based on Bivariate Simplex Splines on Triangle Configurations  Juan Cao, Zhonggui Chen, Xiaodong Wei, Yongjie Jessica Zhang Computer Methods in Applied Mechanics and Engineering, 2019, 357: 112598  [Paper 8M] [DOI]
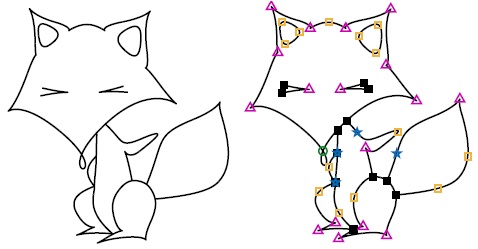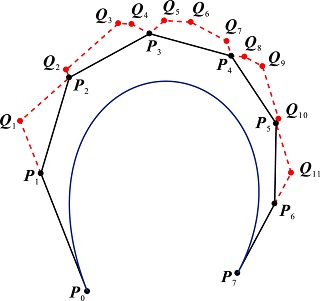
	Interpolatory Curve Modeling with Feature Points Control  Zhonggui Chen, Jinxin, Huang, Juan Cao*, Yongjie Jessica Zhang Computer-Aided Design (Proc. SPM), 114:155-163, 2019  [Paper 1M] [DOI]
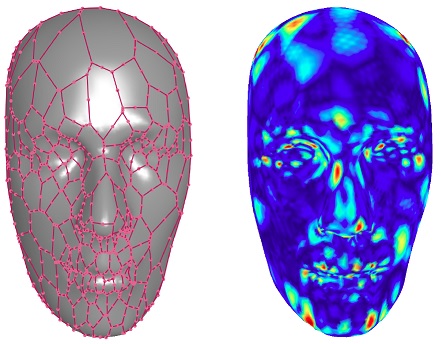
	Identification of two classes of planar septic Pythagorean hodograph curves  Yujun Li, Lincong Fang, Juan Cao, Guozhao Wang Journal of Computational and Applied Mathematics, 348：383-400, 2019 [DOI]
	Functional Data Approximation on Bounded Domains using Polygonal Finite Elements  Juan Cao, Yanyang Xiao, Zhonggui Chen, Wenping Wang, Chandrajit Bajaj Computer Aided Geometric Design, 63:149–163, 2018 [DOI]
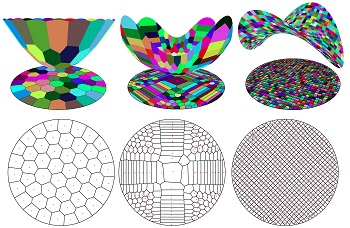	Optimal Power Diagrams via Function Approximation  Yanyang Xiao, Zhonggui Chen, Juan Cao*, Yongjie Jessica Zhang, Cheng Wang Computer-Aided Design (Proc. SPM; Best Paper Award 1st Place), 102:52-60, 2018 [Paper 8M] [DOI]
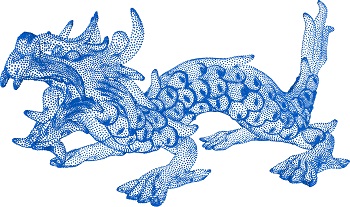	Point Cloud Resampling Using Centroidal Voronoi Tessellation Methods Zhonggui Chen, Tieyi Zhang, Juan Cao*, Yongjie Jessica Zhang, Cheng Wang Computer-Aided Design (Proc. SPM), 102:12-21, 2018 [Paper 14.4M] [DOI]
	Orientation Field Guided Line Abstraction for 3D Printing  Zhonggui Chen, Wen Chen, Jianzhi Guo, Juan Cao*, Yongjie Jessica Zhang Computer Aided Geometric Design (Proc. GMP), 62:253-262, 2018 [Paper 3.6M] [DOI]
	Line Drawing for 3D Printing   Zhonggui Chen, Zifu Shen, Jianzhi Guo, Juan Cao*, Xiaoming Zeng Computers & Graphics (Proc. SMI), 66: 85-92, 2017 [DOI]
	Surface reconstruction using simplex splines on feature-sensitive configurations   Yuhua Zhang, Juan Cao*, Zhonggui Chen, Xiaoming Zeng Computer Aided Geometric Design, 50: 14-28, 2017
	Bivariate Splines over Triangular Meshes for Freeform Surface Modeling with Sharp Feature  Juan Cao*, Jianmin Zheng Computer-Aided Design and Applications , 14(4):498-506, 2017 (Best Paper Award for CAD'16 - Vancouver, CANADA)
	B-spline Surface Fitting with Knot Position Optimization Yuhua Zhang, Juan Cao*, Zhonggui Chen, Xin Li, Xiaoming Zeng Computers & Graphics (Proc. SMI), 58:73-83, 2016
	Ray–triangular Bézier patch intersection using hybrid clipping algorithm  Yanhong Liu, Juan Cao*, Zhonggui Chen, Xiaoming Zeng Frontiers of Information Technology & Electronic Engineering, 2016, 17(10):1018-1030.
	An Improvement on the Upper Bound of the Magnitudes of Derivatives of Rational Triangular Bezier Surfaces   Yanhong Liu, Xiaoming Zeng, Juan Cao* Computer Aided Geometric Design, 31(5), 265-276, 2014 [Website]  [Paper 10M]
	Approximation by Piecewise Polynomials on Voronoi Tessellation  Zhonggui Chen, Yanyang Xiao, Juan Cao* Graphical Models (Proc. GMP 2014), 76(5), 522-531, 2014 [Paper 10M]
	Isotropic Surface Remeshing Using Constrained Centroidal Delaunay Mesh  Zhonggui Chen, Juan Cao*, Wenping Wang Computer Graphics Forum (Proc. Pacific Graphics), 31(7): 2077–2085, 2012  [Paper 10M]
	Spherical DCB-spline Surfaces with Hierarchical and Adaptive knot Insertion  Juan Cao*, Xin Li, Zhonggui Chen, Hong Qin IEEE Transactions on Visualization and Computer Graphics, 18(8): 1290-1303, 2012 [Website]  [Paper 1.5M]
	Non-uniform B-spline Curves with Multiple Shape Parameters Juan Cao*, Guozhao Wang Journal of Zhejiang University - Science C, 12(10):800-808, 2011 [Paper 0.5M]
	Surface reconstruction using bivariate simplex splines on Delaunay configurations Juan Cao*, Xin Li, Guozhao Wang, Hong Qin Computers & Graphics, 33:341-350, 2009 [Paper 2M]  [Talk 10M]
	A Note on Class A Bézier Curves Juan Cao*, Guozhao Wang Computer Aided Geometric Design, 25: 523–528, 2008 [Paper 0.5M]
	The Structure of Uniform B-spline Curves with Parameters Juan Cao*, Guozhao Wang Progress in Natural Science, 18: 303–308, 2008 [Paper 2M]
	An extension of Bernstein-Bézier surface over the triangular domain Juan Cao*, Guozhao Wang Progress in Natural Science, 17(3): 352-357, 2007
	Relation among C-curves characterization diagrams Juan Cao*, Guozhao Wang Journal of Zhejiang University-SCIENCE A, 8(10): 1663-1670, 2007

2019.01 - 2022.12     National Natural Science Foundation of China (No. 61872308)      PI

2015.01 - 2018.12     National Natural Science Foundation of China (No. 61472332)      Co-PI

2012.01 - 2014.12     National Natural Science Foundation of China (No. 61100105)      PI

2011.04 - 2014.03     Natural Science Foundation of Fujian Province (No. 2011J05007)      PI

2012.01 - 2014.12     National Natural Science Foundation of China (No. 61100107)      Co-PI

2012.01 - 2014.12     Natural Science Foundation of Fujian Province (No. 2012J01291)      Co-PI

---

---

---

---

---

---

---

---

• Attending Academic Conferences

  • 2012.09  Pacific Graphics 2012, Hong Kong
  • 2012.06  Geometric Modeling and Processing 2012, Huangshan, China
  • 2011.11  The 5th CSIAM Geometric Design & Computing, Guangzhou, China
  • 2010.09  Pacific Graphics 2010, Hangzhou, China
  • 2009.08  The 4th CSIAM Geometric Design & Computing, Xiamen, China
  • 2009.06  IEEE International Conference on Shape Modeling and Applications 2009, Beijing, China
  • 2008.06  ACM Solid and Physical Modeling Symposium 2008, Stony Brook, USA
  • 2008.06  IEEE International Conference on Shape Modeling and Applications 2008, Stony Brook, USA
  • 2007.06  ACM Solid and Physical Modeling Symposium, Beijing, China
  • 2007.07 The 3th CSIAM Geometric Design & Computing, Lanzhou, China
  • 2006.08  The 2nd China-Korea Joint Conference on Geometric and Visual Computing, Hangzhou, China

• Visiting

  • Prof. Yongjie Jessica Zhang (Carnegie Mellon University, USA), Sept.07, 2017-Sept. 2018,

  • Prof. Wenping Wang (The University of Hong Kong, Hong Kong), Jun. - Sep. 2012

  • Prof. Jianmin Zheng (Nanyang Technological University, Singapore), Oct. 2011 - Feb. 2012

---

---

---

---

---

---

Single Variable Calculus, Multivariable Calculus, Linear Algebra