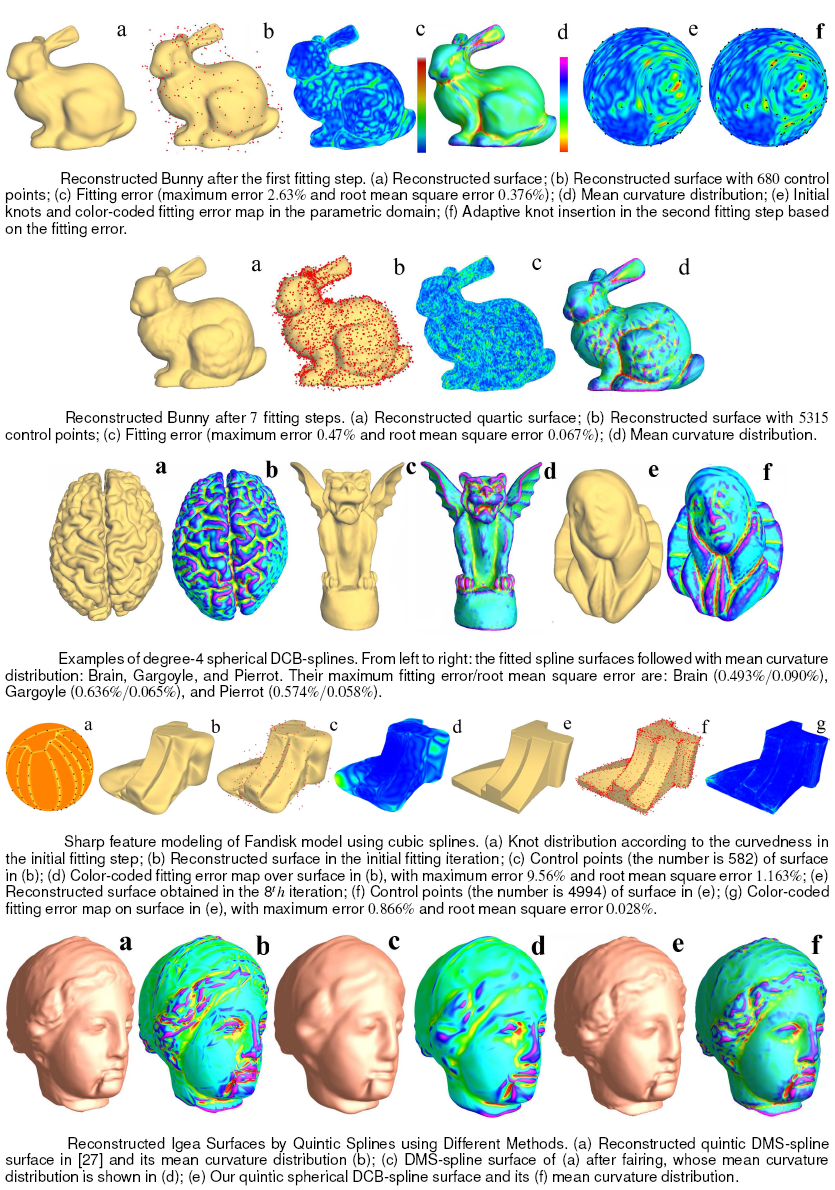
This paper develops a novel surface fitting scheme for automatically reconstructing a genus-0 object into a continuous parametric spline surface. A key contribution for making such a fitting method both practical and accurate is our spherical generalization of the Delaunay configuration B-spline (DCB-spline), a new non-tensor-product spline. In this framework, we efficiently compute Delaunay configurations on sphere by the union of two planar Delaunay configurations. Also, we develop a hierarchical and adaptive method that progressively improves the fitting quality by new knot-insertion strategies guided by surface geometry and fitting error. Within our framework, a genus-0 model can be converted to a single spherical spline representation whose root mean square error is tightly bounded within a user-specified tolerance. The reconstructed continuous representation has many attractive properties such as global smoothness and no auxiliary knots.We conduct several experiments to demonstrate the efficacy of our new approach for reverse engineering and shape modeling.

Keywords: Delaunay Configurations, Spherical Splines, Knot Placement, Knot Insertion, Non-tensor-product B-splines

@article{10.1109/TVCG.2011.156,
author = {Juan Cao and Xin Li and Zhonggui Chen and Hong Qin},
title = {Spherical DCB-Spline Surfaces with Hierarchical and Adaptive Knot Insertion},
journal ={IEEE Transactions on Visualization and Computer Graphics},
volume = {18},
issn = {1077-2626},
year = {2012},
pages = {1290-1303},
doi = {http://doi.ieeecomputersociety.org/10.1109/TVCG.2011.156},
publisher = {IEEE Computer Society},
address = {Los Alamitos, CA, USA},
}