近日,厦门大学计算机图形学课题组完成的一篇最新论文“Quadratic Serendipity Element Shape Functions on General Planer Polygons”被计算力学领域顶级期刊CMAME(Computer Methods in Applied Mechanics and Engineering)录用。CMAME期刊由美国科学院、美国工程院、美国艺术与科学院三院院士、计算力学国际权威专家、等几何分析发明人Thomas J.R. Hughes担任主编,致力于发表流体力学、材料力学、固体与结构力学等计算力学领域的前沿成果。
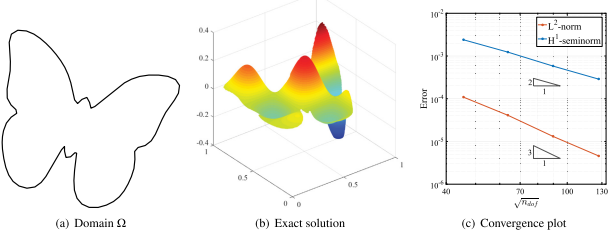
论文提出了一种在平面凸和凹多边形上构造二阶边点元(QSE)形函数的方法。现有用于构造 QSE 形函数的方法是对具有线性精度的广义重心坐标的成对乘积进行线性组合,但这样的构造方法仅限于在凸多边形或通过数值优化得到。我们将QSE形函数的构造方法推广到具有不超过连续三个共线顶点的一般多边形。这是通过将线性组合的系数定义为与多边形域的顶点相关联的三角形的有向面积来完成的,该多边形域可以是凸的或凹的。论文提出的形函数具有二阶精度,并且在给定的几何约束下估计了凸和凹多边形域上基于均值坐标的 QSE 形函数的插值误差。论文中还针对该几何约束定制了一种多边形网格的生成方案,该方案提高了多边形网格的均匀性并有效避免了短边的产生,以便在基于 QSE 的多边形有限元计算中使用。论文最后给出了在不同域上二维泊松方程的数值实验,验证了在 L2-范数和 H1-半范数下误差都达到了最佳收敛。
该论文由课题组成员肖宜、薛飞、曹娟副教授、陈中贵教授,课题组毕业成员目前在南昌大学任教的肖艳阳博士,以及上海交通大学魏小东博士和卡内基梅隆大学Yongjie Jessica Zhang教授共同合作完成。
